Horst Hischer, Braunschweig
Neue Technologien
als Anlaß einer erneuten Standortbestimmung
für den Mathematikunterricht
Zusammenfassung
Die sogenannten "Neuen Technologien" stellen einen bedeutsamen Bildungsgegenstand dar, der jedoch durch bloßen Einsatz des Computers im Unterricht nicht angemessen behandelt werden kann. Vielmehr zeigt eine Erörterung dieses Begriffs, daß Neue Technologien einen Anlaß bilden können, die Aufgabenstimmung von Schule generell zu überdenken, was über den umfassenden Begriff "Technologie" verallgemeinernd zu dem Konzept einer "technologischen Bildung" als einem Aspekt von Allgemeinbildung führt: Hilfen zur verantwortbaren Technikgestaltung vermitteln. Hieraus ergeben sich Konsequenzen auch für eine erneute Standortbestimmung des Mathematikunterrichts, wobei Zusammenhänge zwischen Technologie, Allgemeinbildung und Mathematik einerseits und das Verhältnis von Mathematik und Spiel im Sinne des Schaffens von "Spielräumen" andererseits eine Rolle spielen. Solche "Spielräume" sind erforderlich, um Freiheit und Muße im Bildungsprozeß als Gegengewicht zu kognitiven Aspekten wirksam werden zu lassen. Mathematik kann als Unterrichtsfach einen bedeutsamen Beitrag zur Ausgestaltung solcher Spielräume im Rahmen technologischer Bildung leisten.
Speziell bei den "Neuen Technologien" spielt bei der technologischen Bildung das Verhältnis von Mathematik und Informatik eine Rolle. Zwar sind fundamentale Ideen aus beiden Wissenschaften für den Bildungsauftrag der Schule bedeutsam, jedoch kann das nicht durch zwei Unterrichtsfächer Mathematik und Informatik gelöst werden. Vielmehr ist es sinnvoll, ein gewandeltes Unterrichtsfach Mathematik mit solchen Aufgaben zu betrauen.
Summary
The so called "new technologies" represent a topic which is significant for the class-room. But it is not sufficient to take practise with computers into class-room, because there is somewhat more in this topic. By analyzing the conception of "new technologies" and more generally of "technologies" in terms of philosophy and sociology we arive at the concept of "technological education" as an essential part of general knowledge: learning to make technology assessment with responsibility. This leads us to a new point of view for educational studies in all subjects and in mathematics too. Furthermore, in contrast to cognitive aspects of education it is necessary to offer "time for playing" in the class-room, i. e. not as pure relaxation but as a mental refreshment. Mathematics will do this very good.
In addition the relation between mathematics and computer science is significant for "technological education". There is no reason to introduce a new subject called "computer science" or "information science" at school, since it is sufficient to reform the goals of mathematics education, so that mathematics in school becomes a subject which realizes fundamental ideas of both mathematics and computer science.
1 Einleitung
Im Jahre 1984 bescherte uns die "Bund-Länder-Kommission für Bildungsplanung und Forschungsförderung" das sog. "Rahmenkonzept für die informationstechnische Bildung in Schule und Ausbildung". Dieses Rahmenkonzept war zunächst eine Reaktion auf Aktivitäten in einzelnen Bundesländern. Andererseits zog es in der Folgezeit eine Fülle von Modellversuchen in allen Bundesländern nach sich, und aufgrund der sich abzeichnenden Ergebnisse verabschiedete die Kommission im Jahre 1987 ein "Gesamtkonzept für die informationstechnische Bildung"
(vgl. Bund-Länder-Kommission [3]). Mittlerweile ist es zwar in der bildungspolitischen Szene ruhiger um diese Thematik geworden, jedoch interessieren sich für sie nun mit steigender Tendenz Erziehungswissenschaft, Allgemeindidaktik und Fachdidaktiken. (Die Literatur hierzu wächst stark an. Hier sei nur hingewiesen auf die Zeitschrift für Pädagogik, Jahrgang 1989, Hefte 2 und 5. Von grundsätzlicher Bedeutung ist ferner noch immer die Studie des Rats der Evangelischen Kirche in Deutschland (EKD) aus dem Jahre 1985: Die neuen Informations- und Kommunikationstechniken — Chancen, Gefahren, Aufgaben verantwortlicher Gestaltung, ISBN 3-579-01990-2.)Gleichwohl werden dem Thema noch immer Widerstände und Ressentiments aus Schule und Hochschule entgegengebracht, und ich denke, die sprachliche Entgleisung, die uns in dem Kürzel "ITG" für "informationstechnische Grundbildung" begegnet, ist daran nicht schuldlos. Um es vorwegzunehmen: Ich wende mich zwar entschieden gegen den Gebrauch dieses Kürzels und manche damit zusammenhängenden Fehlentwicklungen, bin jedoch der Auffassung, daß es sich aus curricularer Sicht lohnt, die damit im Zusammenhang oft erwähnten sog. "Neuen Technologien" näher in den Blick zu nehmen, wenngleich dieser Begriff nicht gerade glücklich gewählt ist.
So möchte ich einleitend feststellen, daß diese Neuen Technologien zunächst einen Anlaß bilden (können), die Aufgabenstimmung von Schule im allgemeinen zu überdenken
(vgl. Nieders. Kultusministerium [24]). Eine Erörterung des umfassenden Begriffs "Technologie" führt uns dann verallgemeinernd zu einem Konzept, das ich "technologische Bildung" nenne.Hieraus ergeben sich Konsequenzen auch für eine erneute Standortbestimmung des Mathematikunterrichts, wobei Zusammenhänge zwischen Technologie, Allgemeinbildung und Mathematik eine Rolle spielen.
Mit meinem Beitrag möchte ich zunächst erste Anläufe zur Klärung solcher Zusammenhänge unternehmen, und zwar sind das im einzelnen:
— ein
"Technologische Synergie" als ein Paradigma zeitgemäßer Form menschlicher Kooperation für verantwortbares technisches Planen und Handeln ("Technikgestaltung")
— ein anthropologischer Anlauf
Neue Technologien und Auslagerung von Denkfähigkeit
— ein
allgemeindidaktischer AnlaufDie aktuelle Diskussion um "Allgemeinbildung" und "Bildung" (Klafki)
— ein pädagogischer Anlauf
Notwendigkeit zum Abbau der bisherigen kognitiven Überbetonung
und verstärkte Hinzunahme von "Spielräumen" in den Unterricht
— ein
soziologischer AnlaufDie wachsende Bedeutung von Mathematik für die Gesellschaft im Sinne von:
* "Mathematik ist überall"
* "Mathematik als Technologie"
* "Anwendung von Mathematik"
— ein mathematischer Anlauf
Neue Arbeitsmethoden und Sichtweisen in der Wissenschaft Mathematik, u. a. aufgrund des Computers als einem neuartigen Werkzeug
— ein metamathematischer Anlauf
Grenzen der Anwendbarkeit von Mathematik
, z. B.:*
*
klassische zweiwertige Logik - vage Logik ("Fuzzy Logic")*
beweisbares Wissen - nicht beweisbares Wissen (Gödel)
2 Technologie und Allgemeinbildung,
Mathematik und Spiel, Mathematik und Informatik
— erste Anläufe zur Klärung von Zusammenhängen
Die folgenden Betrachtungen bilden erste, vorläufige Anläufe zur Erschließung der vielfältigen Beziehungen zwischen den Bereichen Technologie, Allgemeinbildung, Mathematik, Informatik und Spiel in ihrem Zusammenwirken.
2.1 Sozialwissenschaftliche Anläufe
2.1.1 Ein philosophisch-sozialwissenschaftlicher Anlauf:
Das Paradigma der technologischen Synergie
Technik — Technologie
Die Begriffe "Technik" und "Technologie" werden häufig unkritisch synonym gebraucht. Englischsprachige Veröffentlichungen tragen sicherlich hierzu bei, weil "technology" durchaus im Sinne von "Technik" verwendet wird (vgl. [12], [13]). Dagegen bedeutet "Techno-Logie" im Sinne des griechischen Wortursprungs sowohl das Verständnis als auch das Wissen von der Technik. In dem somit weit gefaßten Begriff Technologie ist daher bereits die Reflexion über Technik angelegt. Damit kommen wir aber zugleich zu einem philosophisch-sozialwissenschaftlichen Verständnis von Technologie, das ich kurz erläutern möchte.
Nach Auffassung verschiedener Philosophen wie etwa Heinz Hülsmann (Hülsmann [16]) und Walther Ch. Zimmerli (Zimmerli [36], [37]) und Sozialwissenschaftler wie z. B. Arno Bammé (Bammé [1]) ist unsere Gegenwart dadurch gekennzeichnet, daß Wissenschaft und Technik in dem Sinne zusammenwachsen, daß sie eine Synthese in Gestalt der Technologie eingehen - man kennzeichnet dann auch Technologie als Hybrid aus Wissenschaft und Technik: So werden etwa die Naturwissenschaften in dem Sinne techno-logisch, daß die klassischen Abgrenzungen zwischen reiner Wissenschaft, angewandter Wissenschaft und Technik zugunsten einer engen Zusammenarbeit zu verschwimmen beginnen. Wegen der immer komplexer werdenden technischen Situationen kommen die Folgelasten mit ihren räumlich-zeitlichen Dimensionen hinzu, so z. B. im Bereich der Kernenergietechnik und der Gentechnik.
In diesem Sinn gehört dann zur Technologie stets die Reflexion der Folgen technischen Planens und Handelns, was zur Technikfolgenabschätzung führt. Diese kann nun aber ohne Kenntnisse und Methoden aus Sozial- und Geisteswissenschaften einschließlich der Philosophie nicht betrieben werden, wobei insbesondere normative und ethische Kategorien bemüht werden müssen. Somit berücksichtigt ein solches Verständnis von Technologie nicht nur eine Synthese von Wissenschaft und Technik, sondern diese Hybridbildung beinhaltet darüber hinaus eine Integration mit den Sozial- und Geisteswissenschaften.
Technologische Synergie
In dieser Integration wird vielfach ein Paradigmenwechsel gesehen, der mit einem Epochenübergang verbunden ist, und zwar vom wissenschaftlich-technischen zum technologischen Zeitalter. Dieser Paradigmenwechsel ist durch die Notwendigkeit der integrativen Zusammenarbeit aller Kräfte bei der Bewältigung der globalen Existenzfragen gekennzeichnet, also das, was ich technologische Synergie nennen möchte. Technologische Synergie bietet damit eine Chance zur Annäherung der "zwei Kulturen" im Sinne von Charles Percy Snow (Charles Percy Snow in: Kreuzer [22]; ferner z. B. Zimmerli [35]) und sie erfordert von den Beteiligten Kommunikationskompetenz, Kooperationsbereitschaft und das Bewußtsein der Mitverantwortlichkeit, um an den schwierigen Fragen der Technikfolgenabschätzung mitwirken zu können. Es geht also um die Reflexion der Folgen des eigenen Tuns - das "Prinzip Verantwortung". (Jonas [18])
In diesem Sinne wäre dann von Technik zu sprechen, wenn etwa nur die Verfahrens- und Funktionsweisen gemeint sind, von Technologie hingegen, wenn die Technikfolgenabschätzung davon nicht losgelöst wird.
(Zimmerli [38] wies kürzlich nachdrücklich darauf hin, daß "Technikfolgenabschätzung" nur ein Teil einer umfassenderen Aufgabe ist, die man "Technikgestaltung" nennt. Diese besteht aus den Phasen "Technikfolgenforschung", "Technikfolgenabschätzung i. e. S." und "Technikbewertung". Ähnlich wird es in [24], Kap.1, insbes. S. 7 ff, dargestellt.)2.1.2 Ein anthropologischer Anlauf:
Neue Technologien und Auslagerung von Denkfähigkeit
Bei dem Modebegriff "Neue Technologien" ist zu fragen, was denn das Neue daran sein soll und was darunter verstanden werden kann. Folgender Interpretationsvorschlag hilft weiter, indem nämlich das Attribut "neu" nicht auf die Technologien, sondern auf die zugrunde liegenden Techniken bezogen wird. Dabei nehme ich bewußt in Kauf, daß im Alltag auch andere, undifferenzierte Auffassungen vorkommen:
(vgl. [12] und [13])Die auf der Mikroelektronik beruhenden Informationstechniken sind deshalb als "neue" Techniken anzusehen, weil sie über den Mikroprozessor den Computer unserer Zeit hervorgebracht haben, dessen Anwendungsobjekte entgegen dem irreführenden Begriff "Computer" nicht etwa nur Zahlen sind, sondern beliebige Zeichen mit definierter Bedeutung (die man in dem Kontext auch "Symbole" nennt). Damit ist der Einsatzbereich eines Computers prinzipiell universell ("symbolverarbeitende Universalmaschine"):
Jegliche Ansammlungen von Informationen, die in geeigneter Weise binär verschlüsselt werden können, sind von Computern verarbeitbar. Und zu solchen Informationen gehören nicht etwa nur Zahlen, Formeln und Texte, sondern es können Graphiken sein, ferner beliebige, auch farbige, Bilder und Bildfolgen, schließlich auch akustische Informationen wie gesprochene Sprache, Klänge und komplette Musikstücke. Allerdings darf nicht verkannt werden, daß mit einer derartigen binären Verschlüsselung von nicht bereits digital vorliegenden Informationen ein Verlust an Informationsgehalt einhergeht und mithin eine mehr oder minder starke Verzerrung entsteht. (Die Verarbeitung und Übertragung derart digital kodierter Informationen ist dann allerdings prinzipiell verzerrungsfrei möglich - im Gegensatz zur Analog-Verarbeitung.)
Diese universellen Verarbeitungsmöglichkeiten heutiger und erst recht künftiger Computergenerationen sind insofern revolutionär, als hier erstmals nicht wie bei früheren Maschinen mechanische Fähigkeite
n des Menschen im anthropologischen Sinn "ausgelagert" werden (vgl. Fischer/Malle [8], S. 257-258), sondern ein neuer Maschinentypus Fähigkeiten übernimmt, die bisher den menschlichen Geistesleistungen zuzurechnen waren. In diesem Sinn wird gewissermaßen - mit aller gebotenen Vorsicht formuliert - "Denkfähigkeit" auf den Computer ausgelagert.Das begründet die herausragende Stellung der auf der Mikroelektronik beruhenden Informations- (und damit auch der Kommunikations-)techniken und somit ihre "Neuheit", was zu folgender Charakterisierung führt:
Diese Begriffsbildung erweist sich als offen gegenüber künftigen Weiterentwicklungen der Informationstechnik, etwa dem auf dem "Biochip" beruhenden "Biocomputer" oder dem "Optischen Computer", so daß insbesondere der Plural "Informationstechniken" vertretbar ist. Der Zusatz "datenprozessierend" ist erforderlich, damit der bedeutungsreiche Begriff "Information" im vorliegenden Zusammenhang sinnvoll interpretiert werden kann.
2.2 Bildungstheoretische Anläufe
2.2.1 Ein allgemeindidaktischer Anlauf:
Was kennzeichnet heute Allgemeinbildung bzw. Bildung?
Wolfgang Klafki hat sich bekanntlich in besonders umfassender Weise mit der Erörterung des Allgemeinbildungsbegriffs befaßt
(Klafki [19], S. 12-30; [20], S. 9-28). Nach seiner Auffassung sollte sich ein zeitgemäßes Verständnis von Allgemeinbildung in folgendem ausdrücken:Allgemeinbildung als
Seine Vorstellungen können hier nur angerissen werden:
Bildung für alle
Das ist für eine demokratisch verfaßte Gesellschaftsordnung selbstverständlich und somit unmittelbar einleuchtend.
Bildung im Medium des Allgemeinen
Hier geht es um einen verbindlichen Kern dessen, was alle gemeinsam angeht, und zwar mit dem Ziel, daß jeder einzelne ein "geschichtlich vermitteltes Bewußtsein von zentralen Problemen der Gegenwart und - soweit voraussehbar - der Zukunft" gewinne, Allgemeinbildung zeige sich ferner in der "Einsicht in die Mitverantwortlichkeit aller angesichts solcher Probleme" und der "Bereitschaft, an ihrer Bewältigung mitzuwirken".
(Klafki [20], S. 17. - Wir können hier einen Zusammenhang mit dem philosophisch-sozialwissenschaftlichen Anlauf erkennen!) Für solche zentralen Probleme führt Klafki die Bezeichnung "Schlüsselprobleme" ein, z. B. die Friedensfrage, das Umweltproblem, Gefahren und Möglichkeiten der neuen Informations- und Kommunikationstechniken und -medien. (Klafki [20], S. 18. - Hier ist ein Zusammenhang mit dem anthropologischen Anlauf erkennbar!)Damit könnte der Verdacht entstehen, daß hierdurch lediglich kognitive Ziele festgeschrieben werden sollen. Dem begegnet Klafki aber, indem er die Vermittlung "grundlegender Einstellungen und Fähigkeiten" postuliert, die "jeweils inhaltsbezogene und kommunikationsbezogene Komponenten" enthalten (a.a.O.):
- Kritikbereitschaft und Kritikfähigkeit
(einschließlich der Bereitschaft und Fähigkeit zur Selbstkritik)
- Argumentationsbereitschaft und Argumentationsfähigkeit
- Empathie
(die Fähigkeit, eine Situation, ein Problem oder eine Handlung aus der Lage des jeweils anderen, von der Sache Betroffenen aus sehen zu können)
- Bereitschaft und Fähigkeit zu "vernetzendem Denken"
Bildung in allen Grunddimensionen menschlicher Fähigkeiten
Hiermit meint Klafki, daß Allgemeinbildung auch die Eigenschaft vielseitiger Bildung aufweisen
muß (Klafki [20], S. 23). Das bedeutet, daß sich die Schülerinnen und Schüler auch als Individuen mit eigenen Wünschen und Neigungen erfahren müssen.Das leitet über zu meinem nächsten Anlauf:
2.2.2 Ein pädagogischer Anlauf:
Die sog. "Wissenschaftsorientierung" des Unterrichts, die uns vor zwei Jahrzehnten der Deutsche Bildungsrat beschert hat, führte im Zusammenhang mit der "Lernzielorientierung" zu einer kognitiven Übertonung des Unterrichts, die als fatal bezeichnet werden muß.
Zu dieser Einschätzung passen neuere Überlegungen des Erziehungswissenschaftlers Horst Ruprecht (Ruprecht [28], S. 32) die er unter Anknüpfung an Ilya Prigogine (z. B. Prigogine [27]) der Beziehung zwischen Evolution und Pädagogik widmet.
Und zwar weist er darauf hin, daß ein wesentliches Merkmal der Evolution in einer permanenten Erhöhung der Komplexität in der Welt gesehen werden könne. Dieses führe dazu, daß nur die höher entwickelten Lebewesen eine spielerische Entwicklungsphase durchlaufen würden. Insbesondere zeige sich, daß sowohl Dauer als auch Intensität des Spiels geradezu ein Charakteristikum für die Höhe der Evolution seien. In diesem Denkmodell Ruprechts erscheint dann der Mensch "als das am längsten spielende und am meisten des Spielens bedürftige Wesen" (Ruprecht a. a. O.).
Ruprecht leitet hieraus die Forderung ab, daß das Bildungsangebot der Schulen von seinen "sklerotisierenden Rückständen" befreit werden müsse, um sich in allen Fächern wieder für die "Spiel-Räume des Denkens" zu öffnen. (Ruprecht benutzt den Begriff "Spielraum" im Sinne von "spielerischer Freiraum" als freie Übersetzung des griechischen "scholé" für "Muße" (worin ja unser heutiges "Schule" sprachlich weiterlebt). Er ruft damit eindringlich zu mehr Muße in der Schule auf - eine Forderung, die auch Steinberg [31] in seinem Vortrag erhoben hat.) Auch für den Mathematikunterricht entstünden demgemäß besondere Aufgaben:
"Mathematik ist ein grandioses Spiel des Geistes, und als solches müßte sie in den Schulen erscheinen. " (Ruprecht [27], S. 38-39)
Nach den bisher durchgeführten fachübergreifenden Anläufen gelangen wir mit dem letzten zu einer Gruppe fachbezogener Anläufe, welche Zusammenhänge mit der Mathematik herstellen.
2.3 Fachbezogene Anläufe
2.3.1 Ein soziologischer Anlauf:
* Mathematik ist überall
* Mathematik als Technologie
* Anwendung von Mathematik
Hierzu sei in Kürze das Folgende gesagt: Die Mathematik entwickelt sich mit steigender Tendenz zu einem unentbehrlichen Werkzeug in Wissenschaft und Gesellschaft
(Törnig [32] als Vorsitzender der Deutschen Mathematiker-Vereinigung; Maass/ Schlöglmann [23]). Insbesondere entsteht ein neuer Zweig der Mathematik, der mit dem klassischen, aber bereits belegten Begriff "Angewandte Mathematik" nur unzureichend beschrieben wird.In diesem extrem anwendungsorientierten Zweig gibt es Richtungen mit Bezeichnungen wie "Technomathematik", "Industriemathematik" und "Wissenschaftliches Rechnen"
(z. B. Maass/Schlöglmann [23] und Steinberg [30]) und gemeinsam ist ihnen, daß sie als neue mathematische Disziplinen "gegen elementare Regeln und Normen der scientific community" verstoßen, und zwar durch die "Verwendung heuristischer oder experimenteller Methoden" (Kotzmann [21], S.191; vgl. auch Janssen [17]).Ernst Kotzmann mahnt an, daß die Mathematik damit die Rolle einer Technologie im philosophisch-sozialwissenschaftlichen Sinn übernehme und somit Fragen der Technikfolgenabschätzung (bzw. genauer: der Technikgestaltung) in ihre Aktivitäten miteinbeziehen müsse, indem er folgert:
" Dann wird es auch notwendig, in die Technikfolgenabschätzung auch die Abschätzung der Risiken und Folgen mathematischer Aktivitäten miteinzubeziehen. Damit eröffnet sich für die Mathematik die Chance zu einer kritischen Betrachtungsweise, wie sie der Technik und den Naturwissenschaften schon seit längerem von einer breiten Öffentlichkeit entgegengebracht wird." (Kotzmann [21], S. 194)
Mathematiker können sich damit nicht einfach in eine verantwortungsfreie Nische zurückziehen!
2.3.2 Ein (inner-)mathematischer Anlauf:
Neue Sichtweisen und Methoden aufgrund des Werkzeugs "Computer"
Der Computer hat sich mittlerweile zu einem bedeutsamen Werkzeug auch innerhalb der Wissenschaft Mathematik entwickelt. Dazu einige Beispiele:
Der Computer als Trivialisierer
Die Beherrschung arithmetischer Techniken galt einst als anpruchsvolle geistige Leistung – ja gar als ein Merkmal von Bildung. Der Computer – und mit ihm der Taschenrechner – hat solche menschlichen Fertigkeiten entzaubert und sie zur stupiden Rechenarbeit degradiert, die man lieber einer Maschine anvertraut. Bruno Buchberger nennt das "Trivialisierung der Arithmetik durch den Computer"
(Buchberger [2], S. 1). Es handelt sich hierbei im Sinne von Chomsky um den Umgang mit unstrukturierten Daten, zu denen auch Texte gehören. Als Werkzeug nimmt der Computer dabei die klassische numerische Rolle als Rechner, Graphiker und Textverarbeiter wahr.Mittlerweile liegen außerordentlich leistungsfähige Programme vor, mit denen man bereits Elemente der nächsthöheren Sprachschicht – nämlich Bäume und Klammernstrukturen – bearbeiten kann, zu denen u. a. auch Terme und Formeln gehören. Damit tritt der Computer für den Mathematiker in neuen, formalen Rollen auf, nämlich als:
* Termumformer
* Gleichungslöser (algebraisch!)
* Differenzierer (algebraisch!)
* Integrierer (bestimmt/unbestimmt)
Programme, die derartiges leisten können, heißen Formelmanipulationssysteme
(Oberschelp [26]) und sind heute bereits für den PC verfügbar (z. B. DERIVE TM - vgl. etwa Engel [6]). Das bedeutet also, daß damit auch das Gebiet der Formelmanipulation oder des symbolischen Rechnens im Sinne von Buchberger trivialisiert worden ist!Für solche Systeme hat Risch einen Entscheidungsalgorithmus entwickelt, der den Bereich der elementaren transzendenten Funktionen trivialisiert: Dieser Algorithmus liefert für jeden vorgelegten Integranden aus der Klasse der elementaren Funktionen in endlich vielen Schritten eine Entscheidung darüber, ob die zugehörige Stammfunktion derselben Klasse angehört oder nicht, und im positiven Fall wird ein zugehöriger Term auch berechnet. Dieser Algorithmus übertrifft in Verbindung mit heutiger Hardware die menschlichen Leistungen um Größenordnungen (Buchberger [2]).
So ist es nicht verwunderlich, daß auch Hochschulmathematiker derzeit ein großes Interesse an solchen Systemen haben. Die Entwicklung wird wohl über den Prozeß der Miniaturisierung dahin laufen, daß diese Systeme in einigen Jahren auf neuartigen Taschenrechnern jedem preisgünstig zur Verfügung stehen, der "Bronstein" wird dann für den Anwender an Bedeutung verlieren (Oberschelp [26]).
Der Computer als Entdecker
Mit dem Computer liegt für die mathematische Forschung ein neuartiges Werkzeug vor, und zwar für eine experimentelle Mathematik, die es - zumindest in dieser Ausprägung - in der "Vor-Computer-Ära" nicht gab. So kann man über das Spielen mit Formeln und insbesondere mit Algorithmen mathematische Zusammenhänge heuristisch entdecken und Theorien in Wechselwirkung mit dem Computerexperiment entwickeln. Beispiele dafür sind etwa die Chaos-Theorie, die Katastrophen-Theorie, die Fraktale Geometrie und die Theorie dynamischer Systeme, die seit einiger Zeit vielfach Anlaß auch didaktischer Untersuchungen sind.
Der Computer als Beweiser
Das
automatische Beweisen von mathematischen Sätzen, von dem schon Leibniz träumte, ist heute Realität geworden. Dieses wird von sog. Deduktionssystemen geleistet, die häufig auf dem Prädikatenkalkül beruhen, aber auch auf Logiken höherer Stufe. Deduktionssysteme gehören zur sog. "Künstlichen Intelligenz", und sie sind wegen der verwendeten Inferenzmethoden, also Methoden des logischen Schließens, mit den "Expertensystemen" eng verwandt. Die entsprechende Forschergruppe an der Universität Karlsruhe zählt hier mit der von ihr entwickelten "Markgraf Karl Refutation Procedure" zur internationalen Spitze. Gegenwärtig wird daran gearbeitet, ein ganzes mathematisches Lehrbuch durch dieses System beweisen zu lassen, um damit das erste "maschinengeschriebene Mathematikbuch" erzeugen zu lassen (Siekmann [29], S. 95-97).
2.3.3 Ein metamathematischer Anlauf:
Grenzen der Anwendbarkeit von Mathematik
Hier handelt es sich um erkenntnistheoretische Aspekte, die zwar nicht neu, jedoch in bezug auf unser Thema berücksichtigenswert sind.
Mathematische Sprache — natürliche Sprache
Wenn die Mathematik in Bereiche der Realwissenschaften und auch in praktische Wissenschaften Einzug hält und verallgemeinert: wenn Mathematik angewendet wird, so treten Kommunikationsprobleme auf, die nicht nur mit Unterschieden der jeweiligen Fachsprachen, sondern darüber hinaus mit Unterschieden zwischen der formalmathematischen und der natürlichen Sprache zusammenhängen. Man würde heute sagen, die "Schnittstellen" müssen angepaßt werden.
Beispielsweise frage ein Bürger A einen Bürger B:
"Können Sie mir bitte sagen, wie spät es ist?"
Wenn B nun ein "normaler" Mensch mit "gesundem Menschenverstand" ist und hilfsbereit dazu, so wird er selbstverständlich dem Frager die augenblickliche Uhrzeit nennen. Ist B aber beispielsweise ein Mathematiklehrer und A ein Schüler, so wird der Lehrer diesem Schüler möglicherweise - je nach Situation - mit "Ja" oder "Nein" antworten, um damit dem Schüler bewußt zu machen, daß dieser seine Frage unpräzise gestellt habe. Denn das können wir Mathematiker doch: präzise formulieren, und wir wissen auch, wie wichtig das ist, um unsere Theorien bilden und anwenden zu können.
Zugleich offenbart uns dieses Beispiel
Grenzen der Mathematisierbarkeit und damit der Anwendbarkeit von Mathematik, und es führt uns zu dem Forschungsgebiet der "Künstlichen Intelligenz" (KI), die eine typisch technologische Disziplin mit den Aspekten Forschung und Entwicklung ist.Im Rahmen der KI-Forschung erweist sich nämlich die Erforschung der menschlichen, natürlichen Sprache als schwierige Aufgabe
(vgl. v. Hahn [9]; exemplarisch das "Hamburger Redepartner-Modell", v. Hahn [10]). Denn während die Mathematik – wie auch andere Wissenschaften – von der Eindeutigkeit der Begriffe und Aussagen lebt, ist die natürliche Sprache durch Polysemantik gekennzeichnet, weiterhin z. B. durch Vagheit und elliptische Verkürzung.So wird man also vom Selbstverständnis der Mathematik her in ganz besonderer Weise zu berücksichtigen haben, daß der mathematische Denkstil, der von klarer Begrifflichkeit und zweiwertiger Logik – also dem "
tertium non datur" – geprägt ist, großartige Leistungen zu erbringen vermag, daß es daneben aber auch andere Denkstile gibt, die das Menschsein im ganzen erst ausmachen. Beispielsweise die Dichtung lebt geradezu von den eben genannten Eigenschaften der natürlichen Sprache, denn Dichtung will individuell gedeutet und interpretiert werden. Es geht somit um Achtung des andersartigen Denkstils, und solche Fragen wie nach der Uhrzeit sollten in normalen Situationen des menschlichen Miteinander auch von Mathematikern durch assoziatives "Mitdenken" und nicht durch logisch stringente Auslegung beantwortet werden!Klassische zweiwertige Logik — vage Logik
Die Grenzen der mathematischen begrifflichen Eindeutigkeit kommen also bei der natürlichen Sprache klar zum Vorschein und bereiten in der Künstlichen Intelligenz große Probleme. Der amerikanische Mathematiker und Informatiker
Lotfi Zadeh arbeitet seit rund 25 Jahren an der Lösung dieses Problems, indem er einen anderen - in der "scientific community" aber noch nicht anerkannten - Weg geht. (Zadeh [34]; der gebürtige Iraner Zadeh ist Mathematiker und Professor für Informatik an der Universität von Kalifornien in Berkeley.)Zadeh will "mit der Ungenauigkeit der realen Welt fertig werden
" (Zadeh [34], S. 9 ff: "Coping with the Imprecision of the Real World"), denn es klaffe eine große Lücke zwischen der Genauigkeit der klassischen Logik und der Ungenauigkeit der realen Welt. Ich will das in Kürze andeuten:Die meisten "Mengen" in der realen Welt sind keine Mengen im mathematischen Sinn, etwa die "Menge der großen Tiere" oder die "Menge der intelligenten Menschen". Denn die Attribute "groß" und "intelligent" grenzen nicht scharf aus, und so müssen wir im Mathematikunterricht viel Mühe darauf verwenden, den Schülerinnen und Schülern klar zu machen, daß die "Menge der großen Tiere" keine Menge (wohlgemerkt: im Cantorschen Sinn) ist - zumindest mußten wir das!
Auf der anderen Seite können wir Menschen im Rahmen kommunikativen Handelns mit solchen "vagen" oder "unscharfen" Informationen durchaus etwas anfangen, und folglich will man im Rahmen der KI-Forschung derartige Sprachbildungen auch semantisch mit geeigneten mathematischen Mitteln in den Griff bekommen. Während die "normale" KI-Forschung das nun unter Rückgriff auf die zweiwertige Logik versucht, gibt Zadeh diesem Verfahren grundsätzlich keine Chance und hat deshalb seine "
Fuzzy Logic" entwickelt, die im Deutschen z. T. "Unscharfe Logik" heißt und die ich im folgenden kurz mit "Vage Logik" bezeichnen will.Zadeh führt in seiner Theorie zunächst den Begriff der "
Fuzzy Set" ein, die ich "vage Menge" nennen möchte. Anstelle der "scharfen" Elementbeziehung (entweder ist x Element von M oder nicht) verallgemeinert er die zugehörige charakteristische Funktion von dem Wertebereich {0; 1} auf [0; 1] und erreicht damit "unscharfe" bzw. "vage" Elementbeziehungen. Damit kann er dann z. B. die "Menge der großen Tiere" bilden, und ein bestimmtes Element gehört dann etwa mit dem "Möglichkeitswert" 0,7 - also 70% - zu dieser "Menge", die - natürlich - keine Menge im Cantorschen Sinn ist.Zadeh will also die
Vagheiten und Ungenauigkeiten unserer Sprache erfassen, indem er vage Mengen bildet. Zu einer "vagen Logik" kommt er nun, indem er darüber hinaus auch noch vage Quantoren einführt, z. B.: viele – wenige – die meisten – einige – ganz wenige –
viel mehr als 10 – eine große Anzahl – sehr wenige – ...
Durch solche vagen Quantoren, die beliebig gebildet werden können, unterscheidet sich Zadehs "Fuzzy Logic" auch deutlich von der "mehrwertigen Logik", die Lukasiewiecz vor über 60 Jahren begründete.
Ferner gibt es in der vagen Logik
vage Wahrheitswerte und vage Wahrscheinlichkeiten, z. B.: es ist ziemlich wahr – es ist mehr oder weniger wahr –
es ist wenig wahrscheinlich – es ist durchaus möglich – ...
Zadeh führt hierzu aus, daß auf diese Weise die vage Logik ein System bilde, das hinreichend flexibel und ausdrucksreich sei, um einen Rahmen für die Semantik natürlicher Sprachen zu liefern.
Zusammenfassend besteht also seine Idee in folgendem:
Die Aussagen der natürlichen Sprache und die Informationen über die reale, uns umgebende Welt sind in der Regel vage, ungenau und unscharf. Mit Hilfe der vagen Logik sollen diese Vagheiten formal erfaßt und mittels Schlußfolgerungsregeln zu neuen Informationen verarbeitet werden. Diese Ergebnisinformationen sind naturgemäß ebenfalls vage.
In der Fachpresse wird berichtet, die Japaner würden mittlerweile die vage Logik in erheblichem Umfang technisch anwenden
(Chaouli [4], [5]). So werde z. B. nördlich von Tokio eine U-Bahn von einem Computersystem mit unscharfer Logik gesteuert, was dazu führe, daß die üblichen Ruckbewegungen beim Anfahren entfiehlen und ca. 10% Energie eingespart würde. Und der Elektronikkonzern SONY habe neuerdings ein Fernsehgerät im Angebot, das - paradoxerweise - auf unscharfe Weise für größere Bildschärfe sorge.Ich will und kann hier nicht bewerten, ob die Vage Logik sich als wissenschaftlich seriös und als wirtschaftlich erfolgreich erweisen wird.
(Immerhin gibt es in Deutschland bereits zwei wissenschaftliche Hochburgen für Fuzzy Logic: Prof. Dr. Dr. Hans-Jürgen Zimmermann an der TH Aachen und Prof. Dr. Rudolf Kruse an der TU Braunschweig. Im Zusammenhang mit der Fuzzy Logic hat sich die für Anwendungen wichtige "Fuzzy Control" entwickelt, die von Prof. Dr. E. H. Mamdani, University of London, erfunden wurde. In der Jahresmitte 1991 findet an verschiedenen Orten in Deutschland das "1. Deutsche Fuzzy-Logic-Symposium" statt, mit den Referenten Zadeh, Mamdani und Zimmermann). Entscheidend sollte jedoch sein, daß wir uns bewußt sind, wie einseitig doch die von uns üblicherweise verwendete Logik ist und wie weit sie von der Logik der natürlichen Sprache entfernt ist. Damit können wir uns – und vor allem unsere Schüler! – davor bewahren, die Möglichkeiten des mathematischen Denkstils im Diskurs mit anderen zu überschätzen. Einsicht in die Grenzen führt zugleich zu einer Stärkung der eigenen Möglichkeiten.Beweisbares Wissen — nicht beweisbares Wissen:
Im Zusammenhang mit der Bewußtmachung der eigenen Grenzen muß noch die – nicht neue – Erkenntnis erwähnt werden, daß der Mathematik als Mittel zur Wahrheitsfindung deutliche Grenzen gesetzt sind. So besagt ja der Unvollständigkeitssatz von Kurt Gödel aus dem Jahre 1931, daß es mathematische Behauptungen gibt, die weder bewiesen noch widerlegt werden können, was bedeutet, daß eine derartige unentscheidbare Behauptung nicht als letzte Aussage irgendeines Beweises erscheinen kann. Daraus folgt, daß sich die Auffassung mathematischer Wahrheit von der Auffassung mathematischer Beweisbarkeit unterscheidet. Die entscheidende erkenntnistheoretische Schlußfolgerung hieraus ist bekanntlich, daß die mathematischen Systeme formalen Denkens nicht stark genug sind, alles zu beweisen, was wahr ist. Das bedeutet nun, daß es ein Wissen gibt, das nicht aus dem formalen Denken resultiert!
3 Mathematikunterricht und Technologische Bildung
— erste Thesen für eine Standortbestimmung
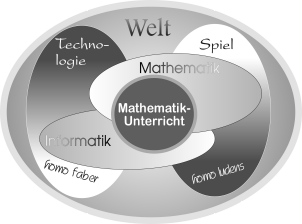
Unter Berücksichtigung der vorausgegangenen "Anläufe" soll nun die Idee einer "technologischen Bildung" skizziert werden, indem ich Thesen formuliere, mit denen ausgewählte Aspekte von Allgemeinbildung betont werden. Dabei ist vorauszuschicken, daß zwar Technologie im hier verstandenen philosophisch-sozialwissenschaftlichen Sinn bedeutsam für die Auswahl von Bildungsgegenständen und die Vermittlung von Haltungen und Einstellungen sein kann, daß aber im Sinne Ruprechts dieses nicht zu einer eindimensionalen kognitiven Ausrichtung führen darf, sondern vielmehr das Spiel eine unverzichtbare weitere Dimension von Allgemeinbildung sein muß. "Technologie" und "Spiel" dürfen damit im Sinne ganzen Menschseins als allgemeinbildende Dimensionen nicht getrennt werden. Dazwischen stehen Mathematik und Informatik als Bindeglieder, und hieraus ergibt sich eine neue Standortbestimmung für den Mathematikunterricht:

Ich bündele meine Betrachtungen in den zehn folgenden, vorläufigen Thesen:
Technologie als Dimension von Allgemeinbildung
1. These: Ein gegenwärtiges Schlüsselproblem der Menschheit ist aufgrund der mittlerweile gewachsenen Einsicht in die globalen Wirkungen und Zusammenhänge menschlichen Planens und Handelns die Sicherung der existentiellen Grundlage der künftigen Generationen. Ein Vertrauen auf "Selbstheilungskräfte der Natur" muß hier zunehmend in Frage gestellt werden, stattdessen ist gemeinsames technologisches Planen und Handeln der Menschen in Wahrnehmung ihrer Verantwortung gegenüber den Mitmenschen und der Schöpfung erforderlich ("technologische Synergie").
2. These: Technologische Synergie erfordert die Mitwirkung von Idealwissenschaften (Mathematik, Philosophie), Realwissenschaften (Naturwissenschaften und Kulturwissenschaften unter Einschluß der Sozialwissenschaften) und praktischen Wissenschaften (Ingenieurwissenschaften). Die an die "technologische Synergie" untrennbar gebundene Verantwortlichkeit der Mitwirkenden erfordert die Ausbildung ethischen Urteilsvermögens. Hierzu gehören auch Einsichten in die Grenzen des fachlich Möglichen und ethisch Zulässigen.
3. These: Der sich aus der technologischen Synergie ergebende Aspekt von Allgemeinbildung läßt sich kennzeichnen als technologische Bildung und betrifft wegen des Synergieaspekts im Prinzip alle Unterrichtsfächer. Technologische Bildung umfaßt auch stets Umwelterziehung (ökologische Bildung) und Friedenserziehung.
Mathematik als Technologie
und damit:Mathematik als spezielle Dimension von Allgemeinbildung
4. These: Die Mathematik entwickelt sich zu einem unentbehrlichen Werkzeug im Rahmen technologischen Planens und Handelns und zum Erkennen von Wirkungszusammenhängen in der realen Welt. Zum Bildungsauftrag der allgemeinbildenden Schule gehört damit unverzichtbar, den Schülerinnen und Schülern fundamentale Ideen und Methoden der Mathematik nahezubringen, die zum Verständnis der Welt, in der wir leben, hilfreich sind.
5. These: Auch die Wissenschaft Informatik spielt über die Informations- und Kommunikationstechnologien eine bedeutsame Rolle im Rahmen der technologischen Synergie. Eine ihrer wesentlichen fundamentalen Ideen und Methoden ist die Algorithmik. Hierin erweist sich die Informatik als Sprößling der Mathematik, gehört doch der Algorithmus zu den mathematischen Urbeständen. Die während der Zeit des Bourbakismus in der Mathematik in den Hintergrund getretene algorithmische Methode bekommt jedoch im Rahmen neuerer mathematischer Theorien und Anwendungen – Fraktale, Chaostheorie, Katastrophentheorie, Dynamische Systeme – eine bedeutsamere Rolle als je zuvor.
Die Kanonfrage: Mathematik und/oder Informatik?
6. These: Nicht alle wichtigen gesellschaftlichen Bereiche haben ihr direktes verkleinertes Abbild durch ein entsprechendes Unterrichtsfach in der Schule, man denke etwa an Rechtswissenschaft, Medizin, Sozialpädagogik und Architektur. Umgekehrt haben nicht alle traditionellen Unterrichtsfächer ihr Pendant in einer wissenschaftlichen Disziplin, z. B. Englisch und Erdkunde. Das liegt daran, daß man den im Fächerkanon vertretenen Unterrichtsfächern zutraut – und offenbar entweder genau diesen oder zumindest diesen in besonderer Weise – im Rahmen der Allgemeinbildung soviel Transfer zu ermöglichen, daß sich mit ihnen und über sie diese Welt, in der wir leben, erschließen läßt.
7. These: Die erforderliche Vermittlung der genannten fundamentalen Ideen und Methoden aus Mathematik und Informatik kann am besten durch ein Unterrichtsfach erfolgen, das sich dieser Ideen annimmt. Der Mathematikunterricht vermag dieses zu leisten, wenn er künftig in allen Stufen und Bereichen des allgemeinbildenden Schulwesens inhaltlich und methodisch so angelegt wird, daß sich die Einrichtung eines Unterrichtsfachs Informatik erübrigt. Das bedeutet jedoch nicht, daß alles, was heute im Informatikunterricht behandelt wird, in einen künftigen Mathematikunterricht übernommen werden muß.
8. These: Ein solches Unterrichtsfach Mathematik kann diesen Bildungsauftrag nicht erfüllen, wenn es nicht zugleich auch die Grenzen und Beschränktheit der mathematischen und informatischen Weltsicht vermittelt.
Spiel als Dimension von Allgemeinbildung
9. These: Allgemeinbildung als Prozeß muß so angelegt sein, daß nicht nur Wissen und Kenntnisse, Einsichten und Betroffenheit, Fähigkeiten und Fertigkeiten vermittelt werden, um jetzige und künftige Schlüsselprobleme der Welt, in der wir leben und in der wir leben wollen, erkennen und möglichst auch lösen zu können.
Allgemeinbildung als Prozeß muß auch Spielräume bereitstellen, um Freiheit in den Bildungsprozeß zu bringen und die Schülerinnen und Schüler ihr Ich entdecken lassen zu können.
10. These: Mathematik als Idealwissenschaft ist wie die Philosophie a priori nicht auf Nutzen gerichtet und in diesem Sinne nutzlos und ein Glasperlenspiel. Mathematik als Unterrichtsfach kann und muß neben seiner Aufgabe im Rahmen einer technologischen Bildung auch die Möglichkeiten dieses Glasperlenspiels zur Schaffung von Spielräumen nutzen.
Hierzu müssen den Lehrerinnen und Lehrern in ausreichendem Maße sowohl inhaltliche Freiräume als auch Anregungen gegeben werden. Mathematikunterricht kann im Rahmen des Unterrichts an allgemeinbildenden Schulen einen bedeutsamen Beitrag zur Ausgestaltung von Spielräumen leisten. Dieses muß nicht auf Fächer wie Kunst, Musik und Sport beschränkt bleiben!
4 Schlußwort
Mit meinen Ausführungen wollte ich vor allem folgendes deutlich machen:
Eine didaktische Standortbestimmung kann – für welches Fach auch immer – weder allein aus der Sicht dieses Unterrichtsfachs und noch aus der Sicht einer ggf. existierenden Mutterwissenschaft vorgenommen werden. Vielmehr ist es erforderlich, auch übergreifende Standorte zu erklimmen, um damit den Bildungsauftrag der Schule – für die Gesellschaft und das Indivuum – in den Blick nehmen zu können.
Die sogenannten "Neuen Technologien" bieten eine Möglichkeit (unter anderen), einen solchen übergreifenden Standort zu finden, denn sie stellen einen Bildungsgegenstand dar, der die allgemeinbildende Schule in ihrer Gesamtheit angeht. Für den Mathematikunterricht und die Mathematikdidaktik ergibt sich hieraus eine neue Standortbestimmung, die weit mehr nach sich zieht als das Aufzeigen von Einsatzmöglichkeiten des Computers im Unterricht:
Das Konzept der technologischen Bildung beinhaltet vor allem das Folgende:
"Technik" muß den Schülerinnen und Schülern nicht als etwas Hinzunehmendes, sondern als etwas aus einer verantwortungsethischen Haltung heraus zu Gestaltendes erscheinen. Dieses ist eine Aufgabe für Schule insgesamt und damit für nahezu alle Fächer.
Speziell die sog. "Neuen Techniken" mit ihren Bezugswissenschaften Informatik und Mathematik sind als Querschnittstechniken in der zivilisierten Gesellschaft unverzichtbar. Die zeitlosen "fundamentalen Ideen" der Wissenschaften Informatik und Mathematik müssen daher im Unterricht der allgemeinbildenden Schule vermittelt werden. Hierzu bedarf es nicht zweier paralleler Unterrichtsfächer Mathematik und Informatik (denn es gibt noch andere wichtige Aspekte von Schule!). Vielmehr kann ein – gewandeltes – Unterrichtsfach Mathematik diese Aufgaben übernehmen. Ein solches Unterrichtsfach Mathematik ist dann allerdings kein verkleinertes Abbild der Bezugswissenschaft Mathematik (neben dann weiteren möglichen Bezugswissenschaften), wie auch das Unterrichtsfach Erdkunde kein verkleinertes Abbild der Bezugswissenschaft Geographie (neben sowieso schon weiteren Bezugswissenschaften) ist.
Unter Berücksichtigung dieser Überlegungen sollte der Mathematikunterricht – zusammen mit den anderen Unterrichtsfächern – von Jahrgang 1 bis 13 von Grund auf inhaltlich und methodisch überdacht werden. Dieses muß sehr sorgsam und darf nicht hastig geschehen, und es könnte sich damit eine anspruchsvolle und umfangreiche curriculare Aufgabe ergeben.
(Vorschläge für den Mathematikunterricht, die solche Informatikelemente – z. T. auch ohne Verwendung des Computers! – mit einbeziehen, liegen z. B. in [24] vor. Diesen Unterrichtsbeispielen liegen fächerübergreifende "allgemeine Ziele der informations- und kommunikationstechnologischen Bildung" zugrunde, wie sie in [15], [24] und [25] veröffentlicht worden sind.).
5 Literaturangaben
[1] Bamm
É, Arno / Baumgartner, P. / Berger, W. / Kotzmann, E.: Technologische Zivilisation und die Transformation des Wissens. München, 1988.[2] Buchberger, Bruno: Should Students Learn Integration Rules? Technical Report. RISC-LINZ Series no. 89-07.0, March 13, 1989. Johannes Kepler University, A-4040 Linz, Austria.
[3] Bund-Länder-Kommission für Bildungsplanung und Forschungsförderung: Materialien zur Bildungsplanung, Heft 16, Gesamtkonzept für die informationstechnische Bildung. Bonn, 1987.
[4] Chaouli, Michel: Digitale Zerrbilder. In: HIGH TECH, Nr. 8/1990, S. 82-84.
[5] Chaouli, Michel: Fundamentaler Wandel. In: HIGH TECH, Nr. 11/1990, S. 50-51.
[6] Engel, Arthur: Eine Vorstellung von Derive
TM. In: Didaktik der Mathematik (1990)3, S. 165-182.[7] Ermert, Karl (Hrsg.): Was bedeutet heute pädagogischer Fortschritt? - Für eine Auseinandersetzung um Bildungsbegriff und -politik. Loccumer Protokolle 8/1989.
[8] Fischer, Roland / Malle, Günther: Mensch und Mathematik. Mannheim, 1985.
[9] v. Hahn, Walther: Künstliche Intelligenz. SEL-Stiftungs-Reihe 2, Stuttgart, 1985.
[10] v. Hahn, Walther: Was ist Künstliche Intelligenz? In: Der Bundesminister für Forschung und Technologie (Hrsg.): Künstliche Intelligenz: Wissensverarbeitung und Mustererkennung. Bonn, 1988, S. 80-87.
[11] Herget, Wilfried (Hrsg.): Mathematik, Computer und Allgemeinbildung. Mathematikbericht 90/3, Dezember 1990, TU Clausthal, Inst. f. Math., Erzstr. 1, 3392 Clausthal-Zellerfeld (Bericht aus dem Arbeitskreis "Mathematikunterricht und Informatik" der GDM, Herbsttagung 6.-8. Oktober 1989 in Wolfenbüttel).
[12] Hischer, Horst: Allgemeinbildende Schulen und neue Informationstechnologien. In: Erziehungswissenschaft und Beruf, 8. Sonderheft (Tagungsband), S. 50-57, Rinteln, 1988. Abgedruckt auch in: Schulcomputerjahrbuch 1988/89. Stuttgart, 1988.
[13] Hischer, Horst: Neue Technologien in allgemeinbildenden Schulen - Ein Beitrag zur begrifflichen Klärung. In: Schulverwaltungsblatt für Niedersachsen 41(1989)4, S.94-98.
[14] Hischer, Horst: Mathematikunterricht und Technologische Bildung. In: Herget [11].
[15] Hischer, Horst / v. Zimmermann, Thomas: Neue Technologien und Allgemeinbildung. In: Computerbildung. 1990, Heft 2, S.4-7.
[16] Hülsmann, Heinz: Mathematik in der Technologischen Formation. In: Maass/ Schlöglmann [23], S. 110-128.
[17] Janssen, Rainer: Wissenschaftliches Rechnen: Eine neue Wissenschaft und ihre Auswirkungen auf die Mathematik. In: Maass/Schlöglmann [23],
S. 47-56.
[18] Jonas, Hans: Das Prinzip Verantwortung - Versuch einer Ethik für die technologische Zivilisation. Frankfurt, 1984.
[19] Klafki, Wolfgang: Neue Studien zur Bildungstheorie und Didaktik - Beiträge zur kritisch-konstruktiven Didaktik. Weinheim und Basel, 1985.
[20] Klafki, Wolfgang: Grundlinien eines neuen Bildungsverständnisses - oder: Was bedeutet heute pädagogischer Fortschritt? In: Ermert [7], S. 9-28.
[21] Kotzmann, Ernst: Alte Theorie - Neue Praxis. Informationstechnologische Auswirkungen auf die Mathematik. In: Maass/Schlöglmann [23], S. 189-196.
[22] Kreuzer, Helmut: Die zwei Kulturen - Literarische und naturwissenschaftliche Intelligenz - C. P. Snows These in der Diskussion. München, 1987. Erste Auflage Stuttgart, 1967.
[23] Maass, Jürgen / Schlöglmann, Wolfgang (Hrsg.): Mathematik als Technologie? Wechselwirkungen zwischen Mathematik, Neuen Technologien, Aus- und Weiterbildung. Weinheim, 1989 (Tagungsband).
[24] Niedersächsisches Kultusministerium (Hrsg.): Neue Technologien und Allgemeinbildung. Bd. 1: Grundlagen und Bildungskonzept. Hannover, 1989. ISBN 3-88990-005-4.
[25] Niedersächsisches Kultusministerium (Hrsg.): Neue Technologien und Allgemeinbildung. Bd. 11: Mathematik - Anregungen für den Unterricht. Hannover, 1990. ISBN 3-88990-010-0.
[26] Oberschelp, Walter: Rechenverfahren und Formelalgorithmen als Unterrichtsgegenstände. Vortrag am 1.10.1990 auf der 10. Bundesfachleitertagung Mathematik in Burg Gemen. Kurzfassung in: Schriften des Deutschen Vereins zur Förderung des mathematischen und naturwissenschaftlichen Unterrichts e. V., Heft 47, (Bericht zum Tagungsthema: Anwendungen der Mathematik gestern und heute).
[27] Prigogine, Ilya: Vom Sein zum Werden - Zeit und Komplexität in den Naturwissenschaften. München/Zürich, 1985.
[28] Ruprecht, Horst: Spiel-Räume fürs Leben - Musikerziehung in einer gefährdeten Welt (Festvortrag auf der 7. Bundesschulmusikwoche in Karlsruhe 1988). In: Ehrenforth, Karl-Heinrich (Hrsg.): Kongreßbericht 7. Bundesschulmusikwoche Karlsruhe 1988, S. 32-39. Mainz, 1989.
[29] Siekmann, Jörg: Die Spezialgebiete der Künstlichen Intelligenz und ihre Perspektiven. In: Der Bundesminister für Forschung und Technologie (Hrsg.): Künstliche Intelligenz: Wissensverarbeitung und Mustererkennung. Bonn, 1988, S. 88-111.
[30] Steinberg, Günter (Hrsg.): Anwendungen von Mathematik in Wissenschaft und Industrie (diverse Aufsätze zu diesem Thema). Der Mathematikunterricht 36(1990)4, S. 3-55.
[31] Steinberg, Günter: Analysis im Mathematikunterricht des Gymnasiums: Kommt Bewegung in festgefahrene Spuren? (Hauptvortrag während der 25. Bundestagung für Didaktik der Mathematik vom 4.-8. März 1991 in Osnabrück.) Erscheint in: Beiträge zum Mathematikunterricht 1991.
[32] Törnig, W.: Begrüßungsworte des Vorsitzenden der Deutschen Mathematiker-Vereinigung zur Jahrestagung 1988 in Regensburg. In: Mitteilungen der Deutschen Mathematiker-Vereinigung, (1988)4, S. 91-97.
[33] Yager, R. R. et al. (Hrsg.): Fuzzy Sets and Applications - Selected Papers by L. A. Zadeh. New York, 1987.
[34] Zadeh, Lotfi A.: (Diverse Aufsätze zu "Fuzzy Logic") In: Yager et al. [33]
[35] Zimmerli, Walther Ch.: Naturwissenschaften und Geisteswissenschaften - zwei getrennte Kulturen? In: Universitas 1/1987, S. 1-4.
[36] Zimmerli, Walther Ch.: Technik als Natur des westlichen Geistes. In Dürr, H.-P./ Zimmerli, W. Ch. (Hrsg.): Geist und Natur. Bern/München/Wien (1989).
[37] Zimmerli, Walther Ch.: Der Mensch als Schöpfer seiner selbst - Realität und Utopie der Neuen Technologien. In: Kwiran/Wiater: Schule im Bannkreis der Computertechnologie. Braunschweig/Augsburg (1989), S. 81-96.
[38] Zimmerli, Walther Ch.: Technikfolgenabschätzung - Wissenschaft oder Politik? Vortrag anläßlich der Jahressitzung 1991 des Landeskuratoriums Niedersachsen im Stifterverband für die Deutsche Wissenschaft am 14. März 1991.